To find a plane in standard form, you need to find two pieces of information:

• a point on the plane
• a normal vector for the plane.

How you find this information depends on the information you're given. Here's a simple example.

Find the plane parallel to the plane 2x - y + 4z = 2 which intersects the z-axis at z = -1.

Solution: Since the plane intersects the z-axis at z = -1, it contains the point (0, 0, -1). Since it is parallel to the plane 2x - y + 4z = 2, we can use the normal vector to that plane as the normal vector for our new plane, i.e. n = [2, -1, 4]. The equation of the plane is then

2(x - 0) -1(y - 0) + 4(z + 1) = 0

which simplifies to 2x - y + 4z = -4.

Here's a more complicated example.

Find the general equation of the plane through the points P(1, 2, 3),   Q(2, 5, –1)  and   
R(1, 4, 2).

 

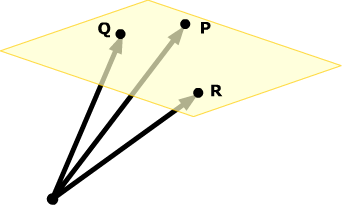
Solution: To help you think, sketch a picture of the situation.You need a point and a normal vector. You have three points to choose from, so you just need to find a normal vector.

 

 

 

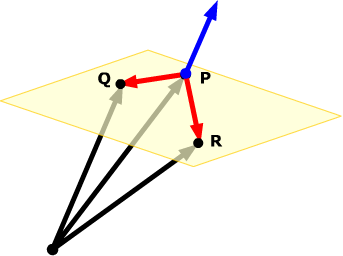
The normal vector will be perpendicular to all vectors in the plane. You have three points in the plane, so you can find several vectors in the plane joining those points. If you take the cross product of any two of those vectors, you will get a vector perpendicular to the plane.

 

 

Find the vectors:   PQ = [1, 3, –4],   PR = [0, 2, –1]

Find their cross product: PQ x PR = [5, 1, 2].

Using P as the point, the plane then has standard form

5(x – 1) + 1(y – 2) + 2(z – 3) = 0.

Multiply out and simplify: 5x + y + 2z = 13.

To find a plane in parametric form, you need

• a point on the plane
• two direction vectors for the plane.

For example, suppose we wanted to find parametric equations for the plane through the points P(1, 2, 3),  Q(2, 5, –1)  and  R(1, 4, 2) of the last example. We have three choices for our initial point, so let's choose P. We can take as direction vectors the vectors
d = PQ = [1, 3, –4] and e = PR = [0, 2, –1]. The parametric equations are then

x = 1 + s
y = 2 + 3s + 2t
z = 3 - 4s - t .

Another example: find parametric equations for the plane containing the line
r =( i + 2j + k) +t(2i - k) and the point P(2, 0, -2).

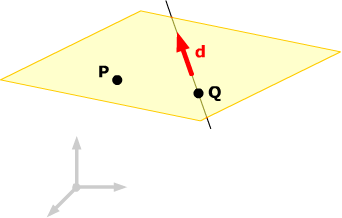
Solution: You already have a point
P(2, 0, -2) on the given plane, and you need two direction vectors. The direction vector for the line is d = 2i - k and a point on the line is Q(1, 2, 1)

It's always a good idea to draw a sketch of the situation. From the sketch, you can see immediately that one of the direction vectors for the plane can be d.

 

 

 

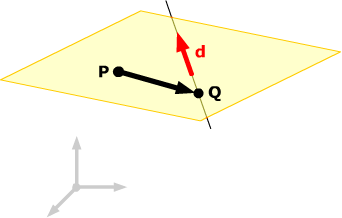
Another direction vector for the plane is not so obvious, but after a little thought, we notice that, since both P and Q are on the plane, so is the vector PQ = [ –1, 2, 3]. Once we choose our second direction vector to be e = PQ, the parametric equations for the plane become

x = 2 + 2s - t
y = 2t
z = -2 - s +3t.