Like lines, planes can be described by giving two pieces of information: a point on the plane (the initial point) and a normal vector - a vector perpendicular to the plane.

 

 

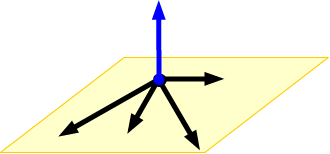
The normal vector fixes the orientation of the plane: all vectors which lie in the plane must be orthogonal to it.

 

 

 

 

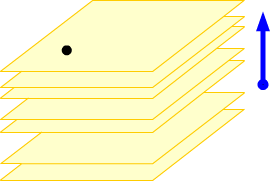
The initial point fixes the location of the plane, and distinguishes it from all the other planes with the same normal vector (which are all parallel to each other).

In the diagram, the plane is fixed. You can change the length of the normal vector to the plane by dragging its head, and change its location by dragging its tail. You can also move the initial point anywhere on the plane.
The normal vector and initial point for a plane are not unique: any non-zero scalar multiple of a given normal vector will work just as well to describe the plane, and the initial point can be any point on the plane.
Suppose that, in some coordinates system, the normal vector is n and the initial point has position vector r0. For a generic point on the plane with position vector r, look at the vector
r - r0.

It lies completely in the plane, so it's orthogonal to the normal vector:

n•(r - r0) = 0.

This equation is know as the point-normal form of the equation of the plane. It can also be written in the form n•r = n•r0 (expand the dot product and rearrange). Note that this equation is a scalar equation. In the next section, we'll expand this equation into a "standard" form.

Using Vectors to Describe Planes
Introduction The point-normal form of a plane The standard equation of a plane The vector equation of a plane Finding planes