It's also possible to represent planes using initial points and direction vectors, much as lines are represented. Think for a moment of a very simple example, the x-y-plane. The position vector of any point in the x-y-plane is a sum of scalar multiples of i and j, so i and j can be considered direction vectors for the x-y-plane.

More generally, for any plane through the origin, if we fix two non-parallel vectors in that plane, the position vector of any point in the plane is a sum of scalar multiples of those two vectors.

In the picture, the position vector of a generic red point on the plane through the origin is the sum of scalar multiples of the two black vectors. The two vectors serve as direction vectors for the plane.

 

 

 

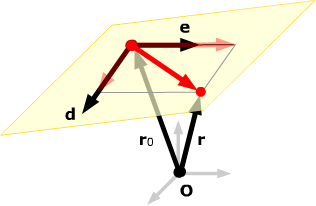
If the plane doesn't pass through the origin, we have to make a further modification: we need to shift the plane and its vectors by adding the position vector of some point on the plane.

 

 

In general, then, we have the following representation: If d and e are non-parallel vectors parallel to a plane and if r0 is any point on the plane, a generic point on the plane has the form

r = r0 + sd + te

for some scalars (parameters) s and t. This equation is called the vector form of the plane. Notice that it's very much like the vector equation of a line, except that it has two direction vectors instead of one.

We can also derive parametric equations for a plane from this vector form. Write all the vectors in terms of their components

r = xi + yj + zk,
r0 = x0i + y0j + z0k,
d = dxi + dyj + dzk
e = exi + eyj + ezk.

Now put put these vectors into the equation r = r0 + sd + te:

xi + yj + zk = x0i + y0j + z0k+ s(dxi + dyj + dzk) + t(exi + eyj + ezk).

Rearrange to get

xi + yj + zk = (x0 + sdx + tex)i + (y0 + sdy + tey )j + (z0 + sdz + tez)k.

Since equal vectors must have equal components, we have

x = x0 + sdx + tex
y = y0 + sdy + tey
z = z0 + sdz + tez.

Notice that the coefficients of s are the components of d and the coefficients of t are the components of e.

It's often useful to be able to convert from one form of plane representation to another.

To convert the standard form ax + by + cz = d of a plane into parametric form: treat the equation as a system of one linear equation in the variables x, y and z and solve it using row reduction. The resulting solution will have two parameters s and t, and will be the parametric form of the plane.

Example: Suppose you're given the plane x + 2y + 3z = 4. Treat this equation as a linear system with one equation. Its augmented matrix is [1, 2, 3 | 4], and is already in reduced row echelon form. Set y = s and z = t, then x = 4 - 2s - 3t, so the solution is

x = 4 - 2s - 3t
y = s
z = t.

To write this parametric form in vector form, first write this solution as

x = 4 - 2s - 3t
y = 0 + 1s + 0t
z = 0 + 0s + 1t.

Then for r0 = [4, 0, 0], d = [-2, 1, 0] and e = [-3, 0, 1], the plane has vector equation
r = r0 + sd + te.

To convert the representation of a plane from vector form r = r0 + sd + te to standard form, you need a normal vector and the position vector of a point on the plane. You already have a point r0. You know that the normal vector must be perpendicular to d and e, so you can take the normal vector to be the cross product of the two direction vectors: n = dxe.

Example: suppose you're given the plane with parametric equations

x = 1 + 2s - t
y = s + t
z = -1 - s + 3t.

Then two direction vectors for the plane are d = [2, 1, -1] and e = [-1, 1, 3], so a normal vector is dxe = [4, -5, 3]. Point P(1, 0, -1) is on the plane, so the standard equation of the plane is

4(x - 1) -5(y - 0) + 3(z + 1) = 0

i.e.  4x - 5y + 3z = 1.