A matrix which is in row-echelon form (without the "reduced") is very similar to a matrix in reduced row-echelon form, except that you don't require that the numbers above the leading 1's be zeroes (The numbers below the leading ones must still be zeroes, since each leading one must be further to the right than those below it.) Here's an example.

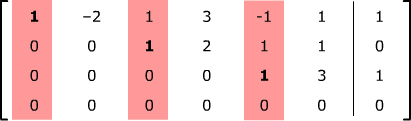
Suppose you've reduced the augmented matrix of your system to the row-echelon form above:

.

There are no bad rows, so you can continue to find the solution. As before, identify the leading variables (corresponding to the leading 1's) and the free variables (the others).

The leading variables are x1, x3 and x5, and the free variables are x2, x4, and x6. Set the free variables equal to parameters:

x2 = s,   x4 = t,   x6 = u.

Now, starting with the bottom non-zero row, translate that row back into an equation and solve for its leading variable in terms of the parameters.

x5 + 3x6 = 1
x5 = 1 – 3u.

Move up to the next row/equation and use your solution for x5 to write x3 in terms of the parameters.

x3 + 2x4 + x5 + x6 = 0
x3 + 2t + (1 – 3u) + u = 0
x3 = –1 – 2t + 2u.

Move up to the next row/equation and use your solution for x3 and x5 to write x1 in terms of the parameters.

x1 – 2x2 + x3 + 3x4 – x5 + x6 = –1
x1 – 2s + (–1 – 2t + 2u) + 3t – (1 – 3u) + u = –1
x1 – 2s – 2 + t + 6u = –1
x1 = 1 + 2s – t – 6u.

The full solution is then

x1 = 1 + 2s – t – 6u
x2 = s
x3 = –1 – 2t + 2u           where s, t and u are parameters .
x4 = t
x5 = 1 – 3u
x6 = u.

Warning: Some textbooks don't require the leading entries in row-echelon form to be 1's - check your text's definition to be sure. (Leading ones are more useful for easy calculations.)

Think of a matrix in row-echelon form as being reduced only "part-way" to reduced row-echelon form. The work you save by reducing the matrix only to row-echelon form is made up for by the extra work you need to do to solve your system, a process known as back substitution. Here's an example to explain the process.