The first key idea for solving linear systems: save writing.

Notice that the variables in a linear system always occur in the same positions in each equation. Instead of writing down all the variables each time you change the system, you can use these positions to keep track of which variable goes where and write down only their coefficients. You put those coefficients and the constant terms of the equations into a rectangular array of numbers, called the augmented matrix of the system.

Here's an example - click the bottom to switch between the system and its augmented matrix.

 

 

 

 

 

The second key idea for solving linear systems: decide clearly just what it is you're allowed to do to the augmented matrix to solve the system.

Without the matrix, you'd multiply equations by constants or add the equations to other equations, for example. With the augmented matrix, you'll do the corresponding operations on its rows: the elementary row operations.

Multiply a row by a non-zero constant:
        Notation: Ri ← cRi  (read as "replace row i by c times row i " for c ≠ 0)

Exchange two rows
        Notation: Ri ↔ Rj  (read as "exchange row i and row j")

Subtract a multiple of one row from another.
        Notation: Ri ← Ri - kRj. (read as "replace row i by itself minus k times row j" for i ≠ j )

The notation is a way for you to keep a record of the row operations you use to solve a system, both to check your work afterward and to inform anyone else trying to follow your work what it is you're doing.

 

Here's a flowchart describing the complete process.

Caution: matrices - rectangular arrays of numbers - are considered to be equal only when they contain exactly the same numbers in each position. When you use row operations to transform a matrix, the result is a different matrix, so don't put an equals sign between them. Matrices which are related by one or more row operations are called row equivalent. If you want, you can use the symbol "~" between matrices to show that they are row equivalent.

Once you've transformed the augmented matrix into a simple enough form, you can translate it back into a linear system again. Your new system will have the same solutions as the old one, since the row operations you did on the augmented matrix just correspond to adding equations, multiplying them by constants or rearranging their order.

What you need to know to proceed is

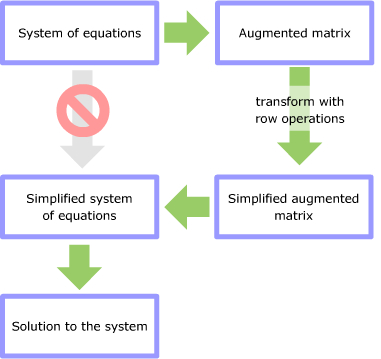
• what exactly is the "simplified augmented matrix" you want to transform to?
• how do you transform to that simplified form?
• how do you solve the simplified system

The first and last questions are answered on the next two pages. The second question is answered in the learning object How to Row Reduce a Matrix.