To find the equation(s) of a line, in any form, you always need two pieces of information:

• a point on the line you can use for your initial point

• a vector in the appropriate direction you can use as a direction vector.

How you find these depends on what information you are given. Below are a few simple examples.

Example: Find parametric equations for the line through the origin parallel to the line

x = 3 - 4t
y = -2 + 7t
z = 5.

Solution: You need a point on the line and a direction vector for the line.

• You're given that the line you want passes through the origin, so you can choose (0, 0, 0) as your initial point.

• You're told that the line is parallel to the given line. Parallel lines have parallel direction vectors, so you can use the direction vector of the given line for your new line. That direction vector is [-4, 7, 0].

The required line is thus

x = 0 + (-4)t y = 0 + 7t                 i.e.   z = 0 + 0t

x = -4t y = 7t z = 0.

Example: Find parametric equations for the line through the points P(1, –2, 3) and
Q(4, 0, –3).

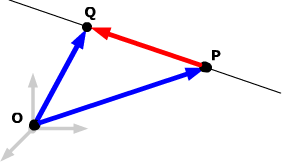
Solution: Draw a sketch (always useful!). To find a line, you need both an initial point and a direction vector. You have two points to choose from, but you need to find a direction vector.

From the sketch you can see that the vector PQ lies along the line and so can be used as a direction vector. Calculate:                   PQ = 3i + 2j –6k, so, using P for the point, the line has parametric equations: x = 1+ 3t y = –2 + 2t z = 3 – 6t