In this diagram, you can change the direction of the line by dragging the head of the direction vector. You can change the position of the line by dragging its initial point.

Notice that parallel lines have parallel direction vectors.

Any line, whether in 2-space or in 3-space, can be described by giving two pieces of information:
     • a single point on the line (called the initial point)
     • a vector giving the direction of the line (called a direction vector)

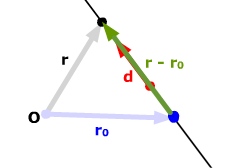
Look at the vector r - r0. It's parallel to the direction vector, and so must be a scalar multiple of it:

r - r0 = td

for some scalar t. Solve for r:

r = r0 + td .

 

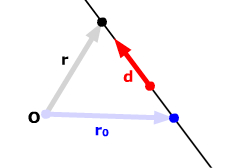
Now let's see if we can derive an equation for a line. Label the direction vector d. Let r be the position vector for a generic point on the line, and let r0 be the position vector for the initial point.

 

 

 

 

 

 

 

 

 

 

Let's look at vector equations for some special lines in 2-space and 3-space.
  • If a line passes through the origin of the coordinate system, you could choose its initial point to be r0 = 0. The vector equation of the line would then have form r = td, i.e. the position vectors of all points on the line are multiples of the direction vector. (This would not be true if you chose some other initial point on the line.)
  • If a line is parallel to the x-axis, you could choose a direction vector d = i, so the line would have equation r = r0 + ti. Similarly, a line parallel to the y-axis could have direction vector j and one parallel to the z-axis, a direction vector k.
  • The direction vector of a line parallel to the x-y-plane cannot have a z-component. The direction vector then must be of the form ai + bj, so such lines have vector equation
    r     = r0 + t(ai + bj).
In this diagram, the line is fixed, but you can change its initial point by dragging it along the line, or change its direction vector by dragging its head, its tail or its shaft.

It's also important to notice that the initial point and direction vector of a line are not unique:

  • the initial point can be any point on the line
  • the direction vector can be any non-zero vector that points in the appropriate direction.
In this diagram, the line, its initial point and its direction vector are fixed. Drag the generic point • to see which parameter values produce which points on the line.≠

If you chose a different direction vector or a different initial point for this line, you would get different values of t for each generic point on the line: the parameter t is tied to your choice of a particular initial point and direction vector.

This equation r = r0 + td describes the position vector of a generic point r on the line in terms of the initial point r0, the direction vector d and a parameter t. Choosing different values of t will give you different points along the line, for example t = 0 gives the initial point.