In 2-space coordinates, lines can be described by a single equation:
Ax + By = C or y = mx + b or any one of several other variations of this equation. In 3-space coordinates, it isn't possible to describe a line by a single equation, at least, not a single scalar equation. To describe lines in 3-space, we need to use vector equations.

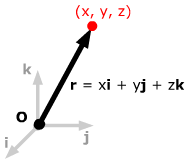
The basic idea: you describe a generic point on the line by giving its position vector with respect to the coordinate system you're using. So if (x, y, z) is a point on the line, its position vector is
r = xi + yj + zk, and you look for a vector equation involving r to characterize the line.

 

 

 

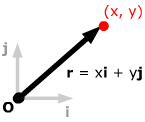
This approach also works in 2-space: a point (x, y) has position vector r = xi + yj, and you need a vector equation involving r to characterize the line. So, as a bonus, using vectors gives you another method of describing lines in 2-space.

In this learning object, we'll look at various ways of describing lines in 2-space and in 3-space:

1. by a single vector equation involving a direction vector for the line and a point on the line
2. by a set of two or three parametric equations
3. by a set of symmetric equations

We'll then look at some examples of how to find lines, and a physical interpretation of the direction vector of a line.